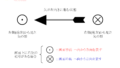
図に巻線の起磁力分布を示す。これは,2極,2層,重ね巻,集中巻となる電機子巻線の一相分による空間的な起磁力分布であり,方形波で表される。フーリエ解析によれば,この方形波起磁力は基本波,第3次高調波,第5次高調波などの奇数次高調波の重畳により表される。
電機子巻線一相の直列巻数を ${w_1}$,電流を ${i_{\text{a}}} = \sqrt 2 \,{I_0}\cos{\omega t}$,$\omega = 2\pi f$ とすれば,一極あたりの方形波起磁力の振幅 ${F_{\text{a}}}$ は次式となる。
$${F_{\text{a}}} = \frac{{{w_1}{i_{\text{a}}}}}{{2p}} = \frac{{{w_1}}}{{\sqrt 2 p}}{I_0}\cos \omega t$$
巻線の起磁力分布 ${f_{\text{a}}}$ を電気角 $\theta $ についてフーリエ級数展開すると,